RELATION BETWEEN PARAMETERS AND ROOTS POSITION
(QUADRATIC)
By Dario Gonzalez Martinez
For this section, we will consider again the quadratic function
![]()
However, this time we will analyze the effects of
parameters a, b
and c on the roots’ position (and
existence) of f(x).
The analysis that I would like to offer here
is related to the approach utilized in Assignment
2 “Parabola’s Parameters Effects.” In other words, I shall utilize the relation
between f(x) and the linear function:
![]()
To explain how parameters a,
b and c affect the roots’
position and existence of the quadratic function f(x). Hence, it becomes
appropriate to recall the Statement 1 written in Assignment
2
“Parabola’s Parameters Effects”:
Statement 1: Given a parabola
![]() and a linear function
and a linear function ![]() , the graph of
the function h(x) = f(x) + g(x) is a
parabola like
, the graph of
the function h(x) = f(x) + g(x) is a
parabola like ![]() , but its graph
will be tangentially positioned on
the linear function
, but its graph
will be tangentially positioned on
the linear function ![]() at x = 0.
In other words,
at x = 0.
In other words, ![]() is a parabola tangent to
is a parabola tangent to ![]() at x = 0.
at x = 0.
Given that Statement 1 is always true, we just
need to imagine what would happen with the parabola when the line (linear
function) changes its y-intercept (parameter c) and its slope (parameter b). These effects are shown below in animations
1(a) and 1(b) (see analysis in Assignment
2 for more details):
|
|
|
|
|
Animation 1(a) (changing parameter c) |
Animation 1(b) (changing parameter b) |
In order to simplify our analysis, we will
consider the effects of parameter a
separate from the effects of b and c.
Before the effects of parameter a are being analyzed, we will consider a > 0 unless we say
something different.
RELATION
BETWEEN THE PARABOLA’S ROOTS AND PARAMETER c
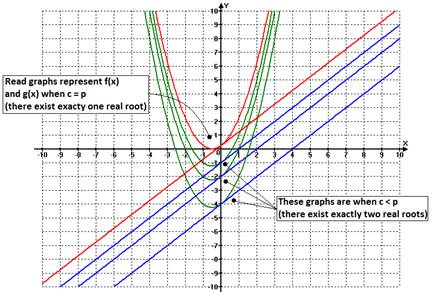
We begin with an example. Consider the function
![]()
We already know that f(x) is tangent with ![]() at x = 0.
So, by reconsidering the animation 1(a), we can easily intuit that the
parabola will have, at least, one real root when
at x = 0.
So, by reconsidering the animation 1(a), we can easily intuit that the
parabola will have, at least, one real root when ![]() for some
for some ![]() .
.
|
|
|
Figure 1 |
We can find p for our example by applying the discriminant
“rule.” We know that a quadratic
function ![]() will have one real root (double root) if and
only if
will have one real root (double root) if and
only if ![]() (this expression is called Discriminant). In other words, we need to find p such that
when c = p, a = 1 and b = 1, then D = 0.
(this expression is called Discriminant). In other words, we need to find p such that
when c = p, a = 1 and b = 1, then D = 0.
![]()
![]()
![]()
![]()
Thus, the quadratic function ![]() will have real roots if and only if
will have real roots if and only if ![]() .
.
After discussing the existence of the parabola’s
roots of our example, we will discuss the location of these roots according to
the variation of parameter c.
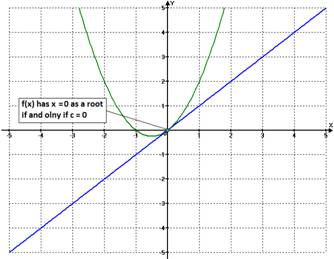
Given that the parabola ![]() is always tangent to
is always tangent to ![]() at x = 0, the parabola will have x = 0 as a
root if and only if c = 0.
at x = 0, the parabola will have x = 0 as a
root if and only if c = 0.
|
|
|
Figure 2 |
This is an important observation because we
can conclude the location of the parabola’s roots by considering the values ![]() and
and ![]() as the “change
points.” That is, by reconsider
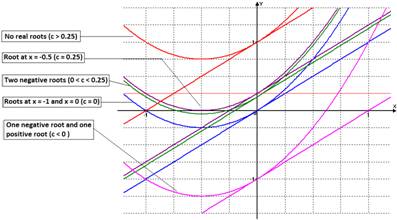
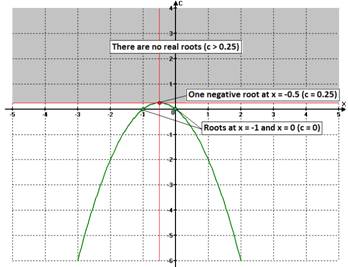
again the animation 1(a), we can easily see that if:
as the “change
points.” That is, by reconsider
again the animation 1(a), we can easily see that if:
·
![]() f(x) has no real
roots.
f(x) has no real
roots.
·
![]() f(x) has one negative
root at
f(x) has one negative
root at ![]() .
.
·
![]() f(x) has two negative
roots.
f(x) has two negative
roots.
·
![]() f(x) has roots at
f(x) has roots at ![]() and
and ![]() .
.
·
![]() f(x) has a negative
root and a positive root.
f(x) has a negative
root and a positive root.
The figure 3 below shows graphically our above
summary:
|
|
|
Figure 3 |
Thus, after discussing the existence and
location of our parabola’s roots, we are going to consider the graph of the
expression
![]()
That is
![]()
In the XC plane drawn
below:
|
|
|
Figure 4 |
This graph gives us the relation between the location (and
existence) of the roots of ![]() for different values of parameter c.
We can appreciate there all what we discussed before.
for different values of parameter c.
We can appreciate there all what we discussed before.
RELATION
BETWEEN THE PARABOLA’S ROOTS AND PARAMETER b
Now we are going to consider the following
quadratic function to lead our analysis of parameter b:
![]()
We are going to remember the relation between ![]() and
and ![]() when b
changes its value by the below animation:
when b
changes its value by the below animation:
|
|
|
Animation 2 |
The newly presented animation allows us to make
a successful conjecture again. The
existence of the parabola’s roots depend on the slope of g(x), so we can
conclude that the parabola has real roots when b = r for some ![]() . Again, we can use the discriminant
to find this r since we know that if a
= 1, b = r and c = 1, then D = 0:
. Again, we can use the discriminant
to find this r since we know that if a
= 1, b = r and c = 1, then D = 0:
![]()
![]()
![]()
![]()
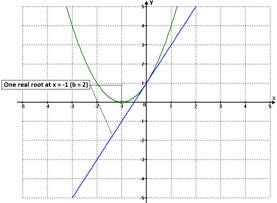
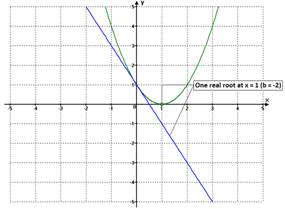
Given the seesaw
effect of the linear function g(x)
when its slope varies; it is reasonable having two values for b such that f(x) has one real root
(double root). We can see this in figure
5 below:
|
|
|
|
|
Figure 5(a) |
Figure 5(b) |
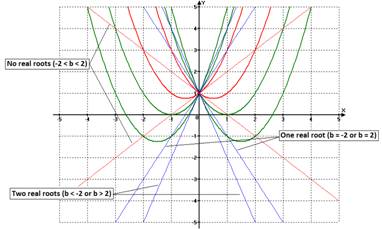
After find the values of b that result in one real root for our parabola, we can elaborate
an analysis about the existence of the roots for ![]() according to the values of b.
The effect of b on the linear function is a seesaw effect; hence, the discussion of the parabola’s roots
existence can be summarized as follow:
according to the values of b.
The effect of b on the linear function is a seesaw effect; hence, the discussion of the parabola’s roots
existence can be summarized as follow:
·
No real roots for -2 < b < 2.
·
One real root for either b = -2 (at x = 1) or
b = 2 (at x =-1).
·
Two real roots for either b < -2 or b >
2.
|
|
|
Figure 6 |
At the same time and given the characteristics
of the parameter b effect, we can
draw easily the conclusion about the location of the parabola’s roots as
follow:
·
Two positive roots when b < -2.
·
One positive root at x = 1 when b = -2.
·
One negative root at x = -1 when b = 2.
·
Two negative roots when b > 2.
There is an important observation related to
one of the final comments written in assignment 2, which holds:
Comment 2: The function ![]() will have a root at x = 0 if and only if c =
0.
will have a root at x = 0 if and only if c =
0.
According to the newly presented comment, we
should consider the animation below:
|
|
|
|
|
Animation 3(a) |
Animation 3(b) |
We can see that as the value of b increase (more than 2), the higher
negative root of the parabola is approaching to x = 0. However, x = 0 is the limit for the higher
parabola’s root, so it never becomes x = 0.
A similar reasoning could be drawn when the value of b decrease (less than -2) for the
smaller parabola’s root. Given that c = 1 in our example, our intuition says
us that having a root at x = 0 implicates that b should be infinite which does not make sense for our analysis.
Thus, after discussing the existence and
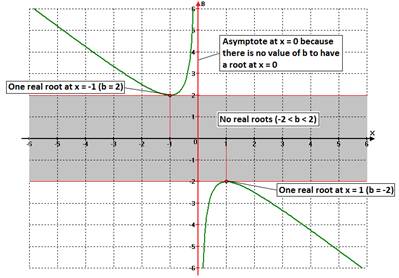
location of the parabola’s roots when parameter b varies, we are going to consider the graph of the expression
![]()
That is,
![]()
In the XB
plane below:
|
|
|
Figure 7 |
This graph gives us the relation between the location (and
existence) of the roots of ![]() for different values of parameter b.
Note the asymptote at x = 0, which indicates that f(x) has no root at x = 0 according to what we discussed before.
for different values of parameter b.
Note the asymptote at x = 0, which indicates that f(x) has no root at x = 0 according to what we discussed before.
RELATION
BETWEEN THE PARABOLA’S ROOTS AND PARAMETER a
Finally we are going to discuss the effect of
parameter a on the parabola’s
roots. In other words, we will discuss
the existence and locations the parabola’s roots when parameter a varies.
Similarly to the prior analysis, we are going
to start with an example. Consider the
quadratic function
![]()
Once again, we need to remember the graphic
effect of changing parameter a’s value and the relation with the linear function ![]() . See the animation below:
. See the animation below:
|
|
|
Animation 4 |
One more time we intuit, by observing the
animation, that there is a value of parameter a which establish the “point
of change” between having real roots and having no real roots for f(x).
We can check the latter intuition by
considering the discriminant of f(x). Suppose that the mentioned “point of change” appears when a = s for some ![]() , then D = 0 for a = s, b = 1 and c = 1.
, then D = 0 for a = s, b = 1 and c = 1.
![]()
![]()
![]()
![]()
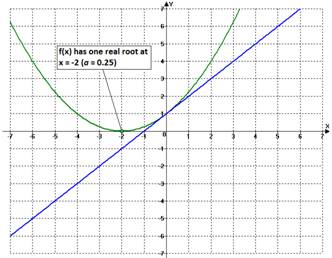
Therefore, when ![]() the parabola has one real root (double root)
at x = -2 as it is shown in figure 8 below:
the parabola has one real root (double root)
at x = -2 as it is shown in figure 8 below:
|
|
|
Figure 8 |
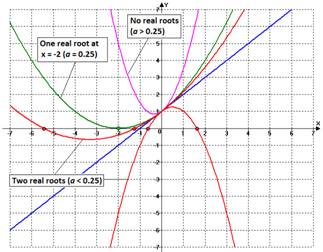
Knowing this “point of
change,” we are capable to discuss the existence of the parabola’s roots
related to the parameter a’s value. This analysis depends on observing what
occurs to the roots in only two cases:
·
When ![]() , there are no
real roots.
, there are no
real roots.
·
When ![]() , there are two
distinct real roots.
, there are two
distinct real roots.
Figure 9 below shows graphically our
conclusion about the existence of the parabola’s roots when parameter a varies.
|
|
|
Figure 9 |
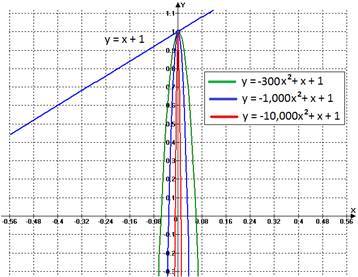
Now for the location analysis of the
parabola’s roots, we should reconsider the animation 4. There we can see that the parabola’s roots
are always negatives while ![]() , and if a = 0 we obtain the linear function
, and if a = 0 we obtain the linear function ![]() (so, there is no parabola at all). However, the most interesting part is when a < 0. We already know, by comment 2, that the
parabola cannot have a root at x = 0.
Even though the parabola’s roots approximate to x = 0 (for leaf and
right hand simultaneously), they are never going to be located at x = 0
because, for that to happen, our intuition tells us that a should be infinite, which does
not make sense for the problem.
(so, there is no parabola at all). However, the most interesting part is when a < 0. We already know, by comment 2, that the
parabola cannot have a root at x = 0.
Even though the parabola’s roots approximate to x = 0 (for leaf and
right hand simultaneously), they are never going to be located at x = 0
because, for that to happen, our intuition tells us that a should be infinite, which does
not make sense for the problem.
The figure 10 below shows what we just
mentioned:
|
|
|
Figure 10 |
Therefore, in brief, we will have the
following location for the parabola’s roots according to the parameter a’s
value:
·
One negative root if ![]() .
.
·
Two negative roots if ![]() .
.
·
There is no parabola if a
= 0 (actually, we obtain ![]() )
)
·
One negative root and one positive root if a < 0
Note two important observations:
Observation
1: there is no root at x = 0
Observation
2: parameter a must be
nonzero real number
Thus, after discussing the existence and
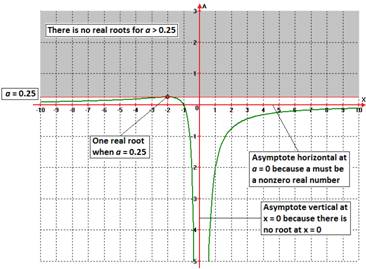
location of the parabola’s roots when parameter a varies, we are going to consider the graph of the expression
![]()
Or similarly,
![]()
In the XA
plane below:
|
|
|
Figure 11 |
This graph gives us the relation between the location (and
existence) of the roots of ![]() for different values of parameter a.
Note the asymptotes at x = 0, which indicates that f(x) has no root at x = 0 according to what we discussed before, and
the asymptote a = 0 because parameter
a must be a nonzero real number
(otherwise, there is no parabola at all).
for different values of parameter a.
Note the asymptotes at x = 0, which indicates that f(x) has no root at x = 0 according to what we discussed before, and
the asymptote a = 0 because parameter
a must be a nonzero real number
(otherwise, there is no parabola at all).
GENERALIZATION
After our discussion about the effect of the
parameters a, b and c on the parabola’s
roots existence and location, we should generalize analysis for any quadratic
function
![]()
Where ![]() .
.
We obviously know if the discriminant of
the quadratic function is D < 0, there are no real roots for f(x).
That is,
Generalization 1: if ![]() then
then ![]() has no real roots (complex roots).
has no real roots (complex roots).
Also, we already know if the discriminant
of the quadratic function is D = 0, there is one real root (double
root) for f(x). That is,
Generalization 2: if ![]() then
then ![]() has one real root.
has one real root.
Finally, we have the most interesting
generalization when the discriminant of the quadratic
function is D > 0. In other words,
Generalization 3: if ![]() then
then ![]() has two distinct real
roots, and they are as follow in table 1:
has two distinct real
roots, and they are as follow in table 1:
*Remember that ![]()
|
|
|
a and b have the same sign |
Two negative
roots |
|
a and b have different signs |
Two positive
roots |
||
|
|
A positive root
and a negative root |
||
|
|
a and b have the same sign |
A root at x = 0
and a negative root |
|
|
a and b have different signs |
A root at x = 0
and a positive root |
||
|
|
The roots are |
||
|
Table 1 |
|||